Scratch

WindozeNT · 2011-11-11 20:30:59

The other day I was using a TI-8x calculator and noticed one of the buttons had an i key. I asked my math teacher what it did and she said it was the square root of negative one (-1). I discovered later that the square root of (-1) did not exist, as well as the square roots of (-2), (-5), (-20) and (-OVER 9000!). I tried to manually find it myself by entering (-1) at a square root prompt. The calculator said "ERROR: NONREAL ANS[WER]". Then I used (-1)*(-1), which returned "1". Then I used i subscript 2, which said -1. Then I tried (-1) subscript 2, which returned 1. However, when I used (-1)*1, I got -1 (despite the fact this isn't the square root of -1 as it isn't the same number)!
I am aware that the square root of (-1) doesn't exist, but I tried to find it. It seems that any negative number is unsquare-rootable. Describe times where you have tried to find the answer to an impossible math function/problem.

EDIT: I think I tried other methods of brain-bending, math-defying expressions in search of (-1)'s square root, but if I did I don't remember them.

Last edited by WindozeNT (2011-11-11 20:38:58)

Harakou · 2011-11-11 20:40:06

How is that a paradox? The square root (or any even root) of a negative number simply doesn't exist as a real number, because squaring any value any number results in a positive number.

i is an "imaginary number" - it exists in concept only, but can still be used to express negative roots. As you have stated, i = sqrt(-1). Therefore, sqrt(-x) = i * sqrt(x).

WindozeNT · 2011-11-11 20:45:59

Harakou wrote:
Therefore, sqrt(-x) = i * sqrt(x).

Is that the solution to the great (-1) question?

MoreGamesNow · 2011-11-11 21:04:29

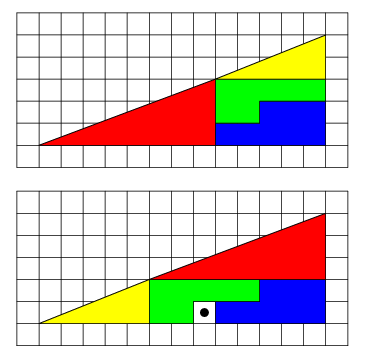
In my opinion, this is a clever "paradox". Anyone see why this works, and what the logical fallacy behind it is?

WindozeNT · 2011-11-11 21:27:06

MoreGamesNow wrote:
http://mathworld.wolfram.com/images/eps … x_1000.gif

In my opinion, this is a clever "paradox". Anyone see why this works, and what the logical fallacy behind it is?

It's due to the specific arrangement of the shapes. But what is that white square with the black dot in the middle? Does that indicate a missing space or is a shape all on its own?

Lar-Rew · 2011-11-11 21:36:01

MoreGamesNow wrote:

In my opinion, this is a clever "paradox". Anyone see why this works, and what the logical fallacy behind it is?

Very nice. Those aren't triangles; the slope of the hypotenuse of the yellow triangle is 0.4, which is greater than 0.375, the slope of the hypotenuse of the red triangle.

Last edited by Lar-Rew (2011-11-11 21:36:19)

MoreGamesNow · 2011-11-12 09:04:43

WindozeNT wrote:
It's due to the specific arrangement of the shapes. But what is that white square with the black dot in the middle? Does that indicate a missing space or is a shape all on its own?

The point is that you are rearranging the same shapes, yet they don't have the same area as the triangle above.

Lar-Rew wrote:
Very nice. Those aren't triangles; the slope of the hypotenuse of the yellow triangle is 0.4, which is greater than 0.375, the slope of the hypotenuse of the red triangle.

Yep smile

jackrulez · 2011-11-12 09:07:27

I find it hilarious that your calculator has an i button yet returns an error for sqrt(-1).

SeptimusHeap · 2011-11-12 09:25:40

Here's one I learned, it will make no sense to people who haven't finished algebra 1 yet:

x=1, y=1
x=y
x²=xy multiplying by x
x²-y²=xy-y² subtracting y²
(x+y)(x-y)=xy-y² using the special difference of squares factoring rule
(x+y)(x-y)=y(x-y) factoring the other side by pulling out y
x+y=y dividing by (x-y)
x=0 subtracting y from each side
but doesn't x=1? so 0=1

QED. can you find the flaw?

Last edited by SeptimusHeap (2011-11-12 09:26:48)

SeptimusHeap · 2011-11-12 09:29:23

Here's (real) proof that .9999999 repeating equals 1 (a simple way)

.9999... / 3 = .3333...
.3333... = 1/3 (fraction)
1/3 * 3 = 1
so .9999 = 1

Lar-Rew · 2011-11-12 09:35:54

SeptimusHeap wrote:
Here's one I learned, it will make no sense to people who haven't finished algebra 1 yet:

x=1, y=1
x=y
x²=xy multiplying by x
x²-y²=xy-y² subtracting y²
(x+y)(x-y)=xy-y² using the special difference of squares factoring rule
(x+y)(x-y)=y(x-y) factoring the other side by pulling out y
x+y=y dividing by (x-y)
x=0 subtracting y from each side
but doesn't x=1? so 0=1

QED. can you find the flaw?

You divided by 0.

Hm... I had a proof that ln(3/2)=2, I think.

maxskywalker · 2011-11-12 09:38:18

Well, as we all learned in our earlier math classes, -1 + (-1) really does equal 1. So does -1 subscript 2. My guess is that the square root of -1 is an imaginary number, because it said 'non-real'. Don't ask me what an imaginary number is.

Last edited by maxskywalker (2011-11-12 09:39:12)

Vista4563 · 2011-11-12 09:44:37

Next time, try the MODE button and select a+bi. This will let you see the numbers that you're talking about.

sqrt[-4]=2i
sqrt[-144]=12i

Enzo1997 · 2011-11-12 10:41:59

No 2 numbers which are the same will ever be multiplied to equal a negative number. Therefore they need to use an imaginary number to solve it.

maxskywalker wrote:
Well, as we all learned in our earlier math classes, -1 + (-1) really does equal 1. So does -1 subscript 2. My guess is that the square root of -1 is an imaginary number, because it said 'non-real'. Don't ask me what an imaginary number is.

-1+(-1)= -2

Last edited by Enzo1997 (2011-11-12 10:43:15)

maxskywalker · 2011-11-12 11:12:23

Harakou wrote:
How is that a paradox? The square root (or any even root) of a negative number simply doesn't exist as a real number, because squaring any value any number results in a positive number.

i is an "imaginary number" - it exists in concept only, but can still be used to express negative roots. As you have stated, i = sqrt(-1). Therefore, sqrt(-x) = i * sqrt(x).

Actually, imaginary numbers actually are just as "real" as integers and doubles. They are only called 'imaginary' because they were originally thought not to exist.

WindozeNT · 2011-11-12 19:35:35

maxskywalker wrote:
Don't ask me what an imaginary number is.

I already know what that is.

P-Cupcake · 2011-11-12 19:59:37

DIVIDE BY ZERO yikes

Harakou · 2011-11-12 20:25:04

maxskywalker wrote:
Harakou wrote:
How is that a paradox? The square root (or any even root) of a negative number simply doesn't exist as a real number, because squaring any value any number results in a positive number.

i is an "imaginary number" - it exists in concept only, but can still be used to express negative roots. As you have stated, i = sqrt(-1). Therefore, sqrt(-x) = i * sqrt(x).
Actually, imaginary numbers actually are just as "real" as integers and doubles. They are only called 'imaginary' because they were originally thought not to exist.

By definition, i is not a real number. A real number, despite the somewhat confusing name, is an actual name given to numbers that can be represented on a continuous number line of traditional numbers. i, defined as the square root of -1, is not a real number because there is no such real number i such that i^2 is equal to a negative number.

Also, from a mathematical standpoint, doubles do not exist. Data types from programming don't perfectly overlap with number types in mathematics, so you shouldn't interchange the two.

maxskywalker · 2011-11-13 07:46:00

jackrulez wrote:
I find it hilarious that your calculator has an i button yet returns an error for sqrt(-1).

+1

maxskywalker · 2011-11-13 07:48:00

Harakou wrote:
maxskywalker wrote:
Harakou wrote:
How is that a paradox? The square root (or any even root) of a negative number simply doesn't exist as a real number, because squaring any value any number results in a positive number.

i is an "imaginary number" - it exists in concept only, but can still be used to express negative roots. As you have stated, i = sqrt(-1). Therefore, sqrt(-x) = i * sqrt(x).
Actually, imaginary numbers actually are just as "real" as integers and doubles. They are only called 'imaginary' because they were originally thought not to exist.
By definition, i is not a real number. A real number, despite the somewhat confusing name, is an actual name given to numbers that can be represented on a continuous number line of traditional numbers. i, defined as the square root of -1, is not a real number because there is no such real number i such that i^2 is equal to a negative number.

Also, from a mathematical standpoint, doubles do not exist. Data types from programming don't perfectly overlap with number types in mathematics, so you shouldn't interchange the two.

I know. Bad choice of words. And I know. I just typed out some numbers off the top of my head, and I was debugging a program in the background.

AtomicBawm3 · 2011-11-13 09:27:22

since we're talking about i....here's a fun fact: e^(i*pi)+1=0

This is a really cool equation because it ties in the 5 most important numbers.

e is the natural base (use the equation 1/0!+1/1!+1/2!... or (1+1/x)^x to find a rough value)
i is the imaginary constant (sqrt(-1) )
pi is half the circumference of a unit circle (a circle whose radius is 1)
1 is the Multiplicative Identity number (i.e. 5*1=5, 4*1=4)
0 is the Additive Identity number (i.e. 4+0=4, 5+0=5)

I would try to explain why this equation is true, but...it would take a HUGE amount of time and most of you probably still wouldn't understand it.

scmb1 · 2011-11-13 10:59:40

AtomicBawm3 wrote:
since we're talking about i....here's a fun fact: e^(i*pi)+1=0

This is a really cool equation because it ties in the 5 most important numbers.

e is the natural base (use the equation 1/0!+1/1!+1/2!... or (1+1/x)^x to find a rough value)
i is the imaginary constant (sqrt(-1) )
pi is half the circumference of a unit circle (a circle whose radius is 1)
1 is the Multiplicative Identity number (i.e. 5*1=5, 4*1=4)
0 is the Additive Identity number (i.e. 4+0=4, 5+0=5)

I would try to explain why this equation is true, but...it would take a HUGE amount of time and most of you probably still wouldn't understand it.

I watched a YouTube video about that a while ago and it is pretty cool. smile Actually, math in general is pretty spectacular, isn't it?

Laternenpfahl · 2011-11-13 12:48:48

SeptimusHeap wrote:
Here's (real) proof that .9999999 repeating equals 1 (a simple way)

.9999... / 3 = .3333...
.3333... = 1/3 (fraction)
1/3 * 3 = 1
so .9999 = 1

1/3 =! 0.33333333333333.....

0.3333 (and so forth) is an approximation

AtomicBawm3 · 2011-11-13 15:28:20

scmb1 wrote:
AtomicBawm3 wrote:
since we're talking about i....here's a fun fact: e^(i*pi)+1=0

This is a really cool equation because it ties in the 5 most important numbers.

e is the natural base (use the equation 1/0!+1/1!+1/2!... or (1+1/x)^x to find a rough value)
i is the imaginary constant (sqrt(-1) )
pi is half the circumference of a unit circle (a circle whose radius is 1)
1 is the Multiplicative Identity number (i.e. 5*1=5, 4*1=4)
0 is the Additive Identity number (i.e. 4+0=4, 5+0=5)

I would try to explain why this equation is true, but...it would take a HUGE amount of time and most of you probably still wouldn't understand it.
I watched a YouTube video about that a while ago and it is pretty cool. Actually, math in general is pretty spectacular, isn't it?

Yup! I don't understand people who hate it.

randomnumber53 · 2011-11-13 18:57:53

0^0

Scratch

archived forums

#1 2011-11-11 20:30:59

The Square Root Of Negative One & Other Crazy Math Paradoxes.

#2 2011-11-11 20:40:06

Re: The Square Root Of Negative One & Other Crazy Math Paradoxes.

#3 2011-11-11 20:45:59

Re: The Square Root Of Negative One & Other Crazy Math Paradoxes.

Harakou wrote:

#4 2011-11-11 21:04:29

Re: The Square Root Of Negative One & Other Crazy Math Paradoxes.

#5 2011-11-11 21:27:06

Re: The Square Root Of Negative One & Other Crazy Math Paradoxes.

MoreGamesNow wrote:

#6 2011-11-11 21:36:01

Re: The Square Root Of Negative One & Other Crazy Math Paradoxes.

MoreGamesNow wrote:

#7 2011-11-12 09:04:43

Re: The Square Root Of Negative One & Other Crazy Math Paradoxes.

WindozeNT wrote:

Lar-Rew wrote:

#8 2011-11-12 09:07:27

Re: The Square Root Of Negative One & Other Crazy Math Paradoxes.

#9 2011-11-12 09:25:40

Re: The Square Root Of Negative One & Other Crazy Math Paradoxes.

#10 2011-11-12 09:29:23

Re: The Square Root Of Negative One & Other Crazy Math Paradoxes.

#11 2011-11-12 09:35:54

Re: The Square Root Of Negative One & Other Crazy Math Paradoxes.

SeptimusHeap wrote:

#12 2011-11-12 09:38:18

Re: The Square Root Of Negative One & Other Crazy Math Paradoxes.

#13 2011-11-12 09:44:37

Re: The Square Root Of Negative One & Other Crazy Math Paradoxes.

#14 2011-11-12 10:41:59

Re: The Square Root Of Negative One & Other Crazy Math Paradoxes.

maxskywalker wrote:

#15 2011-11-12 11:12:23

Re: The Square Root Of Negative One & Other Crazy Math Paradoxes.

Harakou wrote:

#16 2011-11-12 19:35:35

Re: The Square Root Of Negative One & Other Crazy Math Paradoxes.

maxskywalker wrote:

#17 2011-11-12 19:59:37

Re: The Square Root Of Negative One & Other Crazy Math Paradoxes.

#18 2011-11-12 20:25:04

Re: The Square Root Of Negative One & Other Crazy Math Paradoxes.

maxskywalker wrote:

Harakou wrote:

#19 2011-11-13 07:46:00

Re: The Square Root Of Negative One & Other Crazy Math Paradoxes.

jackrulez wrote:

#20 2011-11-13 07:48:00

Re: The Square Root Of Negative One & Other Crazy Math Paradoxes.

Harakou wrote:

maxskywalker wrote:

Harakou wrote:

#21 2011-11-13 09:27:22

Re: The Square Root Of Negative One & Other Crazy Math Paradoxes.

#22 2011-11-13 10:59:40

Re: The Square Root Of Negative One & Other Crazy Math Paradoxes.

AtomicBawm3 wrote:

#23 2011-11-13 12:48:48

Re: The Square Root Of Negative One & Other Crazy Math Paradoxes.

SeptimusHeap wrote:

#24 2011-11-13 15:28:20

Re: The Square Root Of Negative One & Other Crazy Math Paradoxes.

scmb1 wrote:

AtomicBawm3 wrote:

#25 2011-11-13 18:57:53

Re: The Square Root Of Negative One & Other Crazy Math Paradoxes.

Board footer