Scratch
archived forums
#1 2010-04-01 15:08:47
I can prove 1+1=1
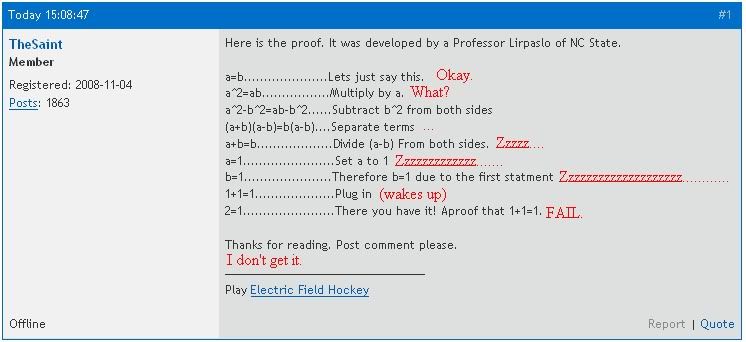
Here is the proof. It was developed by a Professor Lirpaslo of NC State.
a=b.....................Lets just say this.
a^2=ab.................Multiply by a.
a^2-b^2=ab-b^2......Subtract b^2 from both sides
(a+b)(a-b)=b(a-b)....Separate terms
a+b=b...................Divide (a-b) From both sides.
a=1.......................Set a to 1
b=1......................Therefore b=1 due to the first statment
1+1=1....................Plug in
2=1.......................There you have it! Aproof that 1+1=1.
Thanks for reading. Post comment please.
Offline
#3 2010-04-01 15:27:04
- Lucario621
- Community Moderator
- Registered: 2007-10-03
- Posts: 1000+
Re: I can prove 1+1=1
That still doesn't work...
Offline
#5 2010-04-01 15:29:11
#6 2010-04-01 15:35:15
- gettysburg11
- Scratcher
- Registered: 2008-06-14
- Posts: 1000+
Re: I can prove 1+1=1
BWOG wrote:
I got confused on the second statement.
It means that if a=b, then a x a=a x b
All of that made sense except step 4, because (a+b)(a-b) can't equal b(a-b). There's only one variable on the second side, so that would only work if a didn't equal b.
Offline
#7 2010-04-01 15:35:38
- steppenwulf
- Scratcher
- Registered: 2009-07-23
- Posts: 1000+
Re: I can prove 1+1=1
Unless this was some nerdy April Fools joke, that professor needs to go back to kindergarden xD I know it's an April Fools joke
Last edited by steppenwulf (2010-04-01 16:58:36)
I'm graduating HS this April and going to college in the Fall.
Offline
#8 2010-04-01 15:38:02
Re: I can prove 1+1=1
Okay. You start with a=b. That is the base statment. Then, in step two, you multilpy both side by a. This results in a^2=ab. Got it so far? Next step. You subtract both sides by b^2. This leaves you with a^2-b^2=ab-b^2. Next step, the tricky one. You have to separate the terms. (a-b) times (a+b) = a^2-b^2, so therefore we can do the reverse. On the left side, we just pull out a b. Then, you divide each side by (a-b), seeing as it is present on both sides. Finally, you plug in 1 as a and b, and you get 1+1=1 from 1=1.
Math has just been failed.
Offline
#9 2010-04-01 15:39:12
Re: I can prove 1+1=1
gettysburg11 wrote:
BWOG wrote:
I got confused on the second statement.
It means that if a=b, then a x a=a x b
All of that made sense except step 4, because (a+b)(a-b) can't equal b(a-b). There's only one variable on the second side, so that would only work if a didn't equal b.
Your close, just not quite there. If you find it, don't ruin it today.
Offline
#10 2010-04-01 15:45:36
Re: I can prove 1+1=1
In the 5th step, you can't divide by (a-b) because a-b = 0
gettysburg:
(a + b)(a - b)
= a^2 - ab + ab - b^2
= a^2 - b^2
= ab - b^2
= b(a - b)
Last edited by bhz (2010-04-01 15:53:35)
Offline
#11 2010-04-01 15:48:35
- gettysburg11
- Scratcher
- Registered: 2008-06-14
- Posts: 1000+
Re: I can prove 1+1=1
So that means the whole thing is undefined?
Offline
#12 2010-04-01 15:48:54
Re: I can prove 1+1=1
bhz wrote:
no one knows this?
I'm amazed
In the 5th step, you can't divide by (a-b) because a-b = 0
Despite the fact that you ruined my april fools joke, I am happy that someone can do math. That is correct, if you divide by zero, anything can equal another number. Good joob.
Also, Professor Lirpa-slo of NC State? Read the name backwards. You get Fools april, or
APRIL FOOLS!
Offline
#13 2010-04-01 15:55:09
- gettysburg11
- Scratcher
- Registered: 2008-06-14
- Posts: 1000+
Re: I can prove 1+1=1
*smacks self in face* I can't believe I didn't see that.
Offline
#14 2010-04-01 15:57:45
- Lucario621
- Community Moderator
- Registered: 2007-10-03
- Posts: 1000+
Re: I can prove 1+1=1
Yay! I knew it wasn't true (see my post) 
Offline
#16 2010-04-01 16:04:19
- joeisawesome
- Scratcher
- Registered: 2008-06-10
- Posts: 1000+
Re: I can prove 1+1=1
bhz wrote:
In the 5th step, you can't divide by (a-b) because a-b = 0
HOLY CARP YOU JUST DIVIDED BY ZERO
Offline
#19 2010-04-01 17:13:02
Re: I can prove 1+1=1
a+b=b is a contradiction, as are all other statements after it. Therefore, this equation has no solutions.
Offline
#20 2010-04-01 17:22:55
#21 2010-04-01 17:34:31
Re: I can prove 1+1=1
Aidan wrote:
a+b=b is a contradiction, as are all other statements after it. Therefore, this equation has no solutions.
No, that solves for a=0. Seriously. But still, you can't divide by zero, like some other people said.
EDIT: Oh wait, that's what you meant 
Last edited by nXIII (2010-04-02 21:33:00)
Offline
#22 2010-04-01 17:36:41
Re: I can prove 1+1=1
adriangl wrote:
1 is a variable for 0.
One equals the actual number, not a variable.
1+one= 1
Yes, but what about 0 being a variable for 1 
That means that 1 is equal to 0, which just HAPPENS to be equal to 1, which by coincidence is equal to 0, which has a remarkable similarity to 1, which is also quite the same as 0, which is indistinguishable from 1...
Last edited by nXIII (2010-04-01 17:37:03)
Offline
#23 2010-04-01 17:38:50
Re: I can prove 1+1=1
TheSaint wrote:
gettysburg11 wrote:
BWOG wrote:
I got confused on the second statement.
It means that if a=b, then a x a=a x b
All of that made sense except step 4, because (a+b)(a-b) can't equal b(a-b). There's only one variable on the second side, so that would only work if a didn't equal b.Your close, just not quite there. If you find it, don't ruin it today.
I understood it Saint.
Offline
#25 2010-04-01 20:14:49
Re: I can prove 1+1=1
Actually, in Physics, 2+2 can equal 5. I won't go into it though, as it involves Significant digits and the like, which I just don't feel like explaining.
Offline